Before getting into details, you don’t need to be disappointed if you don’t understand the recursion quickly. Initially, it may seem a bit complex or fuzzy to you. But don’t worry, it still seems vague to me. That’s why I will try to write on this topic to make it a little clearer to myself. 🙂
One of the nice real-world examples of recursion I have read in Quora. And it’s written by Thomas Cormen. One of the writers of the famous book Introduction to Algorithm.

Recursion Intro
Recursion is a method/technique to solve programming problems. In simple, recursion is a technique where a function calls itself. Let’s see an example of it.
function func() {
func()
}But at a certain point, this call needs to be stopped. Otherwise, for this infinite recursion, it will throw you a stack overflow error.
There are two main parts to a recursion.
- Base Case
- Recursive Case
The base case defines when to stop the recursion. And it can be one or more than one. On the other hand, recursive cases do the opposite of the base case.
If you can divide your problem into similar subproblems, there is a good chance that you can solve it using recursion. Mainly using recursion, we reduce the problem to a simpler version of itself. And then accumulate all the results for the final solution.
Understanding Recursion Using an Example
Finding the factorial of a number is a good way of understanding recursion.
Let’s assume that we need 5!. How can we get it? If we know the factorial of 4, we can easily get 5!. That is 5 * 4!. Similarly:
4! = 4 * 3!
3! = 3 * 2!
…Let’s try to understand how it works recursively. Let’s assume that we have to function that gives us the factorial of a number. If the function returns 4! and we multiply it by 5, we will get 5!. And this way we are going to solve this problem.
Before that, we have to think about the base case. The base case is generally the smallest solution to a problem. More precisely, it’s simple and directly solvable. In this case, we all know that the factorial of 1 is 1. So if we need to know the factorial of 1, we can directly return 1. We don’t need any further function calls. And this will be the base case.
So whole things work something like below.
Factorial(5) ^ | 5 * Factorial(5-1) ^ | 4 * Factorial(3-1) ^ | 3 * Factorial(2-1) ^ | 2 * Factorial(2-1) ^ | 1 (At this point, we don't need recursive case. Because we are at the base case. And we just return it.) // The formula f(n) = n * f(n-1)
Let’s see the code in Python.
def factorial(n):
# Base Case
if n <= 1:
return n
# Recursive Case
return n * factorial(n-1)
print(factorial(3)) # 6
print(factorial(5)) # 120In the above code, we defined a recursive function to find the factorial of a given number.
First, the function calls for 3, and 3 is greater than the base case. So it will go to the recursive part. Before returning anything, we call the same function for 2 (3-1). Again, number 2 is greater than the base case. And we go to the recursive case. After following the same procedure, now ‘1’ is fulfilled our base case condition. So, this function stop going further and returns 1 to the previous one. Which is 2 * factorial(2-1) (return value is 1). And again, this value will return to the first called function. That is 3 * factorial(3-1) (return value is 2). So the final result is 6.
Pardon my vague explanation. I know it’s a little bit confusing.
Call Stack
You might think, how do these functions store returned value, or what happens when functions are called recursively? These function calls are stored in memory as Stack. It is known as Call Stack. And we all know Stack follows Last In First Out (LIFO). Each time, we call a function. It goes on top of the previous one. And then, the last added one popped first after completing the operation. And so on.
Let’s see a surface-level visual example of Call Stack. We will try to demonstrate the above code example for the value 5.
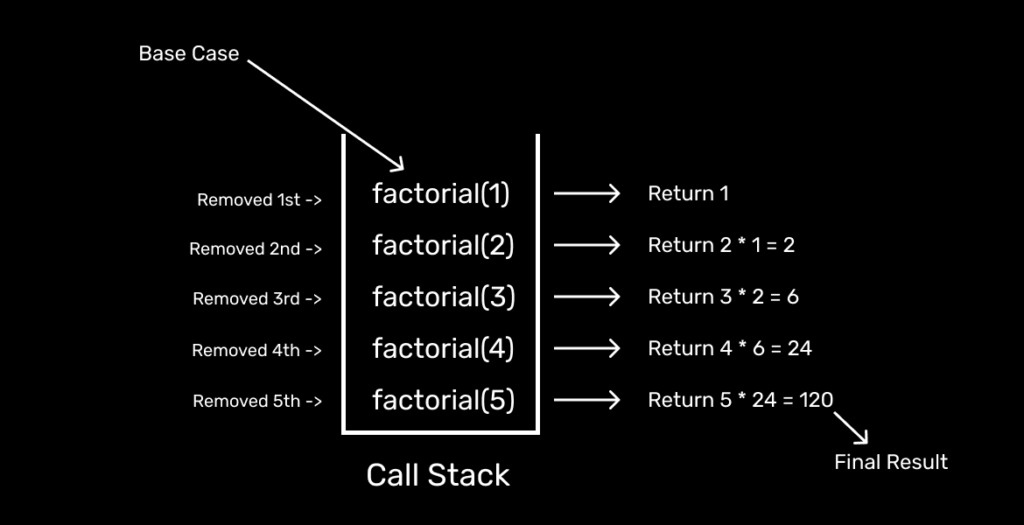
I hope you got the idea of the above visual example.
Last Words
Recursion is one of the best ways to solve problems. Though not all. The efficiency depends on the problem’s type. Such as in terms of performance, the recursive solution for large Fibonacci series is low. But trust me, this is an excellent and helpful method for solving problems.
I know understanding recursion in one blog is not easy. But I try to make it simple. I hope you get a bit of understanding from my blog.
My suggestion is that try to solve recursion-related problems from online problem-solving platforms. Read more about it. Try to understand it in depth.

